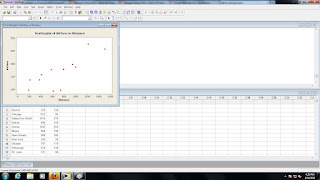
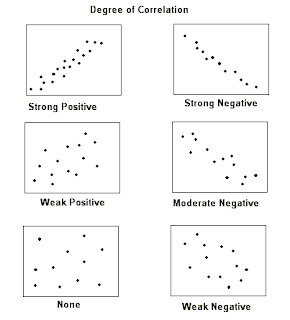
4.2 #24) r = .099. Positive, but no LINEAR association.
#29) Near zero, no linear correlation. As you age, nothing happens to your batting average.
4.3 # 7c) Superspeedway = 18.2 + 0.034(short track)
#9a) 30. Superspeedway = 18.2 + 0.034(30)
Superspeedway = 18.2 + 0.034(30)
Superspeedway = 19.22
Superspeedway = 20 (round up, it doesn't make sense to have 19.22 wins)
#9b) 50. Superspeedway = 18.2 + 0.034(50)
The highest value in the original data set is 46, 50 is extrapolation.
Residual plot - Whether or not the line does as good a job as we can do provided the following criteria are met: 1) same approximate number of observations are above and below the regression line on the residual plot. 2) Totally random, no pattern whatsoever. Looks like someone spilled dots on a plot.
Residual - How much the line is off by from the observation. Residual = (Data point - Predicted value from line).
Residual plot makes your regression plot horizontal to help identify a pattern we may not have
previously seen.
r
2 - Coefficient of Determination (Proportion of Variability) - Tells you how much variability in Y is explained by X
0
< r
2 < 1 ; will not give you direction like r.
r
2 is the proportion of the
variability in Y that is explain by X.
7 Requirements for a Regression
- Display Descriptive Statistics
- Correlation Coefficient (r)
- Scatterplot
- Regression
- Residual (with Residual Plot)
- Unusual Observations (Outliers with respect to regression and influential points)
- Coefficient of Determination (r2)
Data set used in the following examples is available on Blackboard
(In Class> ws3_minitab.zip> WS3_Minitab> Minitab 15 Data> Gestation 06.MTW)
1. Display Descriptive Statistics
Stat> Basic Stats> Display Descriptive Statistics>
Select Variables of Interest>
Select OK>
Analyze each variable to determine the shape of the distribution, compare the location of the Mean relative to the Median.
For Longevity:
Mean (13.55) > Median (12.00). Right-Skewed. Unconvinced? Compare the range at the ends. (Q1-Minimum) and (Maximum-Q3).
(8.0-1.0) and (41.0-15.75), simplifying: 7 and
25.25. There's greater range at the right side, therefore right skewed.
For Gestation:
Mean (194.7) > Median (175.5). Right-Skewed. Unconvinced? Compare the range at the ends. (Q1-Minimum) and (Maximum-Q3).
(64.3-13.0) and (645.0-277.5), simplifying: 51.3 and
367.5. There's greater range at the right side, therefore right skewed.
2. Correlation
Stat> Basic Stat> Correlation>
Select Variables>
OK>
Correlation Coefficient (r) = 0.589.
What does this value tell us about the direction and strength of the linear association? It's a positive value, thus positive direction. The strength is moderate because it's greater than .33 and less than .70.
Unfortunately the correlation coefficient (r) doesn't give us an accurate representation of the data, for that we need a scatterplot.
3. Scatterplot
Graph> Scatterplot
Simple>
Select your variables of interest>
Note: Which one explains the other? The eXplanatory variable (X-Axis) predicts the response variable (Y-Axis).
Select OK>
Now you analyze your scatterplot. You're looking for obvious non-linear patterns. Do the correlation coefficient (r) and scatterplot compliment each other?
4. Regression Equation
Stat> Regression> Regression>
Select your variables of interest>
Note: Which one explains the other? The eXplanatory variable (X-Axis) predicts the response variable (Y-Axis).
Select OK>
Scroll to the top of the output, starting from "The regression equation is:"
Simply rewrite the given equation, in this example the equation for the regression line is:
Gestation = 54.5 + 10.3 Longevity
If given the regression equation can you...
- Identify X? Longevity.
- Identify Y? Gestation.
- Identify the Y-intercept (b0)? 54.5 days.
- Interpret the Y-intercept (b0)? The value for the Y-intercept does not make sense in the context of this regression. If you set Longevity (X) equal 0, you get a gestational period of 54.5 days. It does not make sense for an animal who lives less than a year gestate for 54.5 days.
- Identify the slope coefficient (b1)? 10.3 days.
- Interpret the slope coefficient (b1)? 10.3 days is the predicted change in gestation (Y) for every 1 year change in longevity (X). Alternatively, we predict the gestation will increase 10.3 days for every 1 year increase in longevity.
5. Unusual Observations
Scroll down a little bit in your regression print out>

- Are there any outliers? Yes, three. Observations 18, 22, and 34.
- How can you tell? "R denotes an observation with a large standardized residual" this means that these observations have a standardized residual value greater than ±2 (|2|, absolute value 2).
- What do these outliers mean? These values are outliers with respect to the regression line, they have very large residual which means they are really far away from our fitted line.
- Are there any influential observations? Yes, two. Observations 15 and 22.
- How can you tell? "X denotes an observation whose X value gives it large leverage" Influential observations are generally outliers with respect to the X-Axis (longevity in this example).
- Are any observations outliers and influential observations? Yes, one. Observation 22.
- What do these influential observations mean? If we remove them from our data set the line shifts dramatically.
6. Residual Plot
Stat> Regression> Fitted Line Plot>
Select your variables of interest>
Note: Which one explains the other? The eXplanatory variable (X-Axis) predicts the response variable (Y-Axis).
Select Storage>
Select "Residuals" and "Fits" Select OK> Select OK>
The "Residuals" and "Fits" will be stored in columns adjacent to your original data.
What is a residual? How far the dot is away from the regression line (you can calculate a residual by subtracting the actual observed value from the value predicted by the regression line).
Please note: A negative residual is an overestimate and a positive residual is an underestimate.
Stat> Regression> Fitted Line Plot>
Select Residuals for your Y-Axis and your original X (longevity in this example) for your X-Axis>
Select OK>
Now you analyze your residual plot. You're confirming for two things: 1) equal distribution of observations above and below the regression line and 2) No obvious patterns.
- Are approximately half the observations above the line? Yes.
- Are approximately half the observations below the line? Yes.
- Does there appear to be a pattern? No. The dots are random with no obvious pattern.
Now that the two prerequisites have been satisfied, we can conclude that the regression line is as good as we can do for this data.
7. Coefficient of Determination (r2)
There are a few ways to find r
2 I'll show you the ones you've already found.
- In step 4 (Regression Equation) when you had Minitab output all that regression data it gave you r2
 |
| R-Sq=34.7% |
- In step 6 (Residual) plot when you made the Regression with a fitted line (in order to create your residuals and fits) that graph had
r2 in the upper right hand corner
 |
| R-Sq=34.7% |
- Alternatively, grab a calculator and square the correlation coefficient (r) found in step 2
(.589)^2 = .346921, or .347 after simplifying which can also be expressed as 34.7%
What is r
2? .347 or 34.7%
What does this number tell you? 34.7% of the variability in gestation (Y) is explained by longevity (X).
8. Predictions
Making predictions with your regression equation.
If given a value for X, plug it into your regression equation to determine the predicted Y value.
For example, suppose you knew the average life expectancy (longevity) of an African Honey Badger is 24 years and you wanted to predict how long it gestates.
So we take our regression equation:
Gestation = 54.5 + 10.3 Longevity
Now plug in 24 for Longevity
Gestation = 54.5 + 10.3 (24)
Performing the necessary arithmetic:
Gestation = 54.5 + 247.2
Gestation = 301.7
Gestation = 302 (rounding up because we can't have .7 days)
Our regression equation predicts the gestation period for the African Honey Badger to be 302 days.
Note: The value we entered for longevity (24) was valid because it was within the range of our original data. If we refer back to our descriptive statistics, the minimum for longevity was: 1 and the maximum for longevity was: 41. If we were try to enter a value less than 1 or greater than 41, this would be extrapolation.
Your textbook defines extrapolation as: "using the regression equation to make estimates or predictions based on x-values that are outside the range of x-values in the data set" p.669.
9. Conclusions
Will this line do a good job of explaining gestation (Y)? ("How much stock would you put in this model being accurate?") We are not very confident in this model's prediction ability given the low percentage of variability (provided by r
2).